ロジスティック回帰分析
第二ソリューションの K.S です。
今回はロジスティック回帰分析を調べてみました。
ロジスティック回帰分析は、線型モデル(式1)をシグモイド関数(式2)により確率p(0〜1)へ変換して得られます。
今回はベルヌーイ分布(事象が0、1の2つしかないモデル(式3))に従うモデルを扱います。
真の値(y=0 or 1)と予測値(p)の確率関数の差を交差エントロピー(式4)によって求めます。
この交差エントロピーの最小となるa、bを求めることで分類することができます。
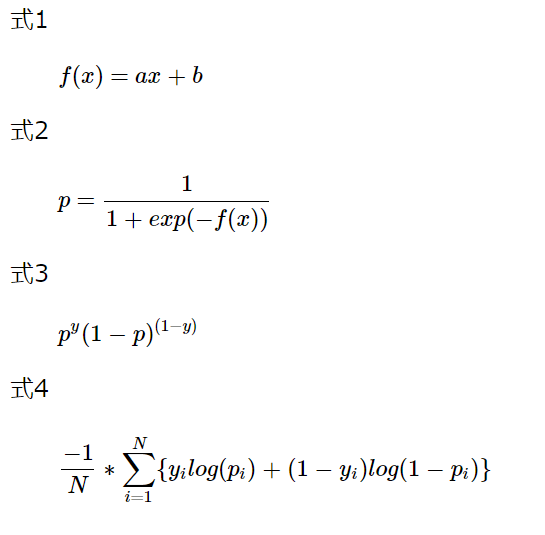
何かサンプルとして使えそうなデータはないものかと探してみました。
そこで、以下のページを参考に通勤時間から大都市圏(1)と都市(0)を分類できないかを試してみることにしました。
大都市ほど通勤時間が長い傾向にあり、通勤時間から大都市、都市を含む都道府県の予測を行います。
https://www.stat.go.jp/data/shakai/2011/rank/rank3.html
上記のデータから CSV 形式のデータを作成しました。Lは大都市、Sは都市を表します。
但し、TASC の事務所がある都道府県(新潟、東京、群馬)は評価値として使用するため除いております。
no,prefectures,commuting time,class
1,kanagawa,100,L
2,saitama,94,L
3,chiba,94,L
5,nara,88,S
6,hyogo,83,L
7,osaka,78,L
8,kyoto,76,L
9,ibaraki,73,S
10,aichi,72,L
11,miyagi,70,L
12,siga,69,S
13,hiroshima,69,S
14,tochigi,67,S
15,mie,67,S
16,wakayama,67,S
17,fukuoka,67,L
18,gifu,66,L
19,okayama,66,L
21,toyama,61,S
22,yamanashi,60,S
23,tokushima,60,S
24,nagasaki,60,S
25,fukushima,59,S
26,nagano,59,S
27,shizuoka,59,L
28,saga,59,S
29,iwate,58,S
30,kagoshima,58,S
31,hokkaido,57,S
32,aomori,57,S
33,akita,57,S
34,yamaguchi,57,S
35,kagawa,57,S
36,kumamoto,57,S
37,okinawa,57,S
38,yamagata,56,S
39,ishikawa,56,S
41,kouchi,55,S
42,tottori,54,S
43,ehime,54,S
44,fukui,53,S
45,ooita,53,S
46,shimane,52,S
47,miyazaki,50,S
次は、scikit-learn を使ったプログラムになります。
LogisticRegression を使い、学習を fit、予測を predict で行います。
係数(coef_)と切片(intercept_)を求めてシグモイド関数のグラフを作成しています。
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LogisticRegression
df_data = pd.read_csv(“data.csv”)
#大都市に1、大都市以外に0を設定
tx = df_data[[“commuting time”]]
ty = df_data[“class”].map({“L”: 1, “S”: 0})
col = [“commuting time”]
ex = [[55], [90], [62]] #新潟(55分)、東京(90分)、群馬(62分)
df_ex = pd.DataFrame(data=ex, columns=col)
lr = LogisticRegression()
lr.fit(tx, ty)
print(“coefficient = “, lr.coef_)
print(“intercept = “, lr.intercept_)
print(“score = “, lr.score(tx, ty))
ey = lr.predict(df_ex)
print(“[新潟 東京 群馬]=”, ey)
nx = np.arange(-5.0, 180.0 , 0.1)
ny = 1/(1 + np.exp(-(lr.coef_[0] * nx + lr.intercept_)))
plt.plot(nx, ny)
plt.show()
結果は以下になります。
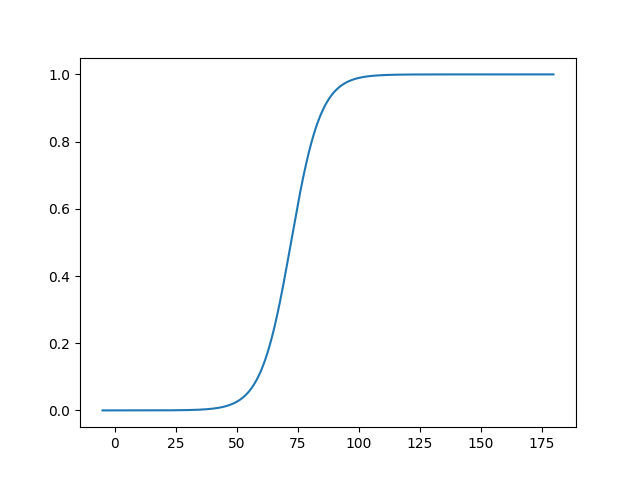
coefficient = [[0.16346042]]
intercept = [-11.81373489]
score = 0.8181818181818182
[新潟 東京 群馬]= [0 1 0]
スコアをみてもそこそこの結果が得られたのではないでしょうか。
まとめ
初回にしては上手くできたと思ったのですが、新潟が大都市圏に含まれていないと予測されています。通勤時間が短いからですが、実際は大都市圏に含まれております。
どのようなデータをどのような手法で分析するのかなど、機械学習の学習を進めて行くにあたって今後の課題だと思いました。