第二ソリューションのK.Sです。
先日、非線形回帰分析の対数線形モデルを学習したのでブログに書こうと思う。
何故、対数線形モデルを学習しようと思ったのかというと、テレビでよく見る日々のコロナ感染者数が曲線を描くように増減しているため、対数線形モデルを使えば上手く予測値が得られるのではないかと思ったからです。
そこで、年末年始の新型コロナ感染者数を調べました。期間は2022/12/28〜2023/01/03までの一週間になります。
28日 216219人
29日 192063人
30日 148784人
31日 107465人
01日 86924人
02日 76264人
03日 89643人
対数線形モデルは以下の式で表せます。
Y=X^(ax+b)
この式を直接扱える API はなさそうです。
そこで底を10(=X)としたとき、この式は log10(Y)=ax+b と同じで単線形回帰分析になります。これなら scikit-learn の LinearRegression で扱えます。
ここで Y はコロナ感染者数、x は1日目、2日目・・・7日目を表します。
log10(Y)は NumPy の関数を使って算出し、a と b は scikit-learn の LinearRegression を使って算出します。
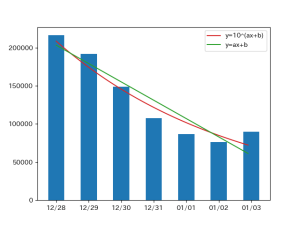
今回は参考のため単線形回帰分析も実行してみました。見た目にも対数線形モデルの方が適しているようです。
曲線を描くようにして増加(減少)するようなデータには利用できそうです。
しかし、世の中にそのような事象は少ないかもしれません。
そこで、また別の機会に別の手法を学習したいと思います。
以下は Python プログラムになります。
import numpy as np
import math
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
corona_cnt = [216219, 192063, 148784, 107465, 86924, 76264, 89643]
x = [1, 2, 3, 4, 5, 6, 7]
Y = np.log10(np.array(corona_cnt))
model = LinearRegression()
model.fit(np.array(x).reshape(-1, 1), Y)
print('Y=10^(ax+b)')
print('a=', model.coef_)
print('b=', model.intercept_)
print('R^2=', model.score(np.array(x).reshape(-1, 1), Y))
x1 = np.arange(1, len(x), 0.1)
y1 = np.power(10, model.coef_ * x1 + model.intercept_)
model.fit(np.array(x).reshape(-1, 1), corona_cnt)
x2 = np.arange(1, len(x), 0.1)
y2 = model.coef_ * x2 + model.intercept_
print('y=ax+b')
print('a=', model.coef_)
print('b=', model.intercept_)
print('R^2=', model.score(np.array(x).reshape(-1, 1), corona_cnt))
x_label = ['12/28', '12/29', '12/30', '12/31', '01/01', '01/02', '01/03']
plt.plot(x1, y1, color='C3', label='y=10^(ax+b)')
plt.plot(x2, y2, color='C2', label='y=ax+b')
plt.bar(x, corona_cnt, width=0.5, tick_label=x_label)
plt.legend(loc=1)
plt.show()
結果
Y=10^(ax+b)
a= [-0.07795704]
b= 5.396990528800588
R^2= 0.884952611531223
y=ax+b
a= [-24042.35714286]
b= 227221.14285714284
R^2= 0.8743796596477873